티스토리 뷰
728x90
반응형
문제
N*N 크기의 게임판이 있을 때, (0, 0)에서 (N-1, N-1)까지 규칙(조건)에 맞게 이동할 수 있는 경로의 수를 구하는 문제이다.
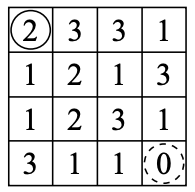
< 그림 1 >
문제 조건
- 각 칸에는 한 번에 이동 가능한 거리가 쓰임
- 반드시 오른쪽 혹은 아래쪽으로 이동
풀이
- 문제의 조건을 주의해야 한다. (오른쪽과 아래쪽으로만 한 번에 직선 이동 가능)
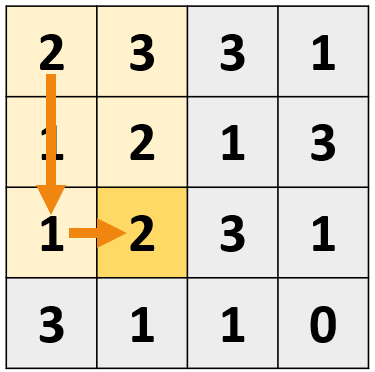
- 오른쪽과 아래쪽으로만 이동 가능하기 때문에 왼쪽 위의 경로의 수를 먼저 구하고 해당 경로의 수를 활용하여 다음 위치의 경로의 수를 구할 수 있다. 즉, DP를 활용할 수 있다.
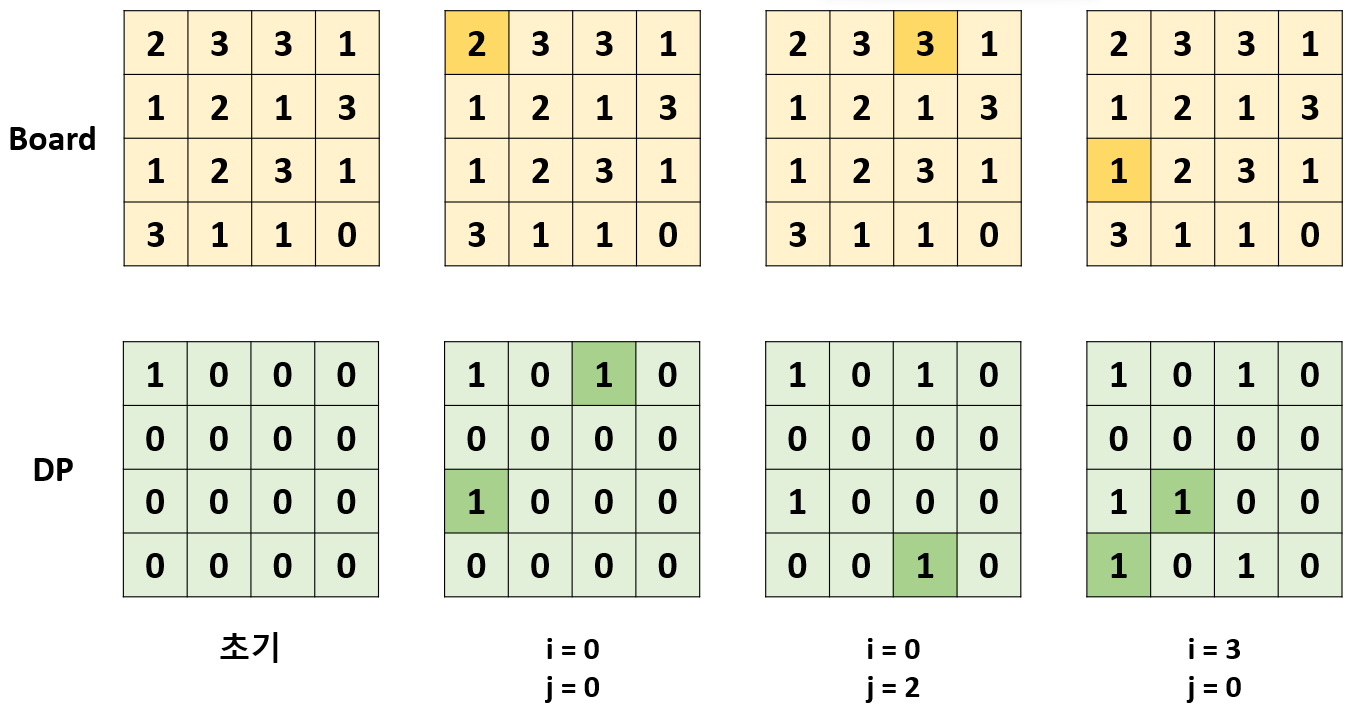

- 위의 그림은 < 그림 1 > 의 예시의 풀이 과정을 시각화한 것이다.
- 각 칸을 방문하면서 게임판의 범위 내에서 이동 가능한 거리라면, DP에 저장되어 있는 현재 위치까지 도달하는데 가능한 경로의 수를 다음 위치에 더해준다.
- 값이 0인 칸은 이동할 수 없다는 점을 유의해야 한다.
- 모든 칸에서의 이동이 끝나면 자동으로 각 칸에 도달하는 경로의 수가 DP에 담기게 된다.
알고리즘
- 경로의 수를 담아둘 DP를 0으로 초기화한다.
- 출발지인 (0, 0) 의 경로의 수를 1로 설정한다.
- 모든 칸을 방문하면서 각 칸에서 조건에 맞게 도달할 수 있는 칸이 존재한다면, 현재 칸의 경로의 수를 다음 칸의 경로의 수에 더한다.
- 가장 오른쪽 아래 칸 (n-1, n-1) 의 경로의 수를 출력한다.
Python 코드
import sys
input = sys.stdin.readline
n = int(input()) # row의 길이
board = [input().split() for _ in range(n)]
m = len(board[0]) # col의 길이
dp = [[0]*m for _ in range(n)]
dp[0][0]=1
def sol():
for i in range(n):
for j in range(m):
k = int(board[i][j])
# 이동 가능한 거리가 0이라면 넘어간다.
# 또는 dp가 0이라는 것은 현재 위치에 도달할 수 없음을 의미함으로 넘어간다.
if k == 0 or dp[i][j] == 0:
continue
if i+k < n: # 아래쪽으로 이동하는 경우, 게임판을 벗어나지 않는다면 경우의 수 추가
dp[i+k][j] += dp[i][j]
if j+k < m: # 오른쪽으로 이동하는 경우, 게임판을 벗어나지 않는다면 경우의 수 추가
dp[i][j+k] += dp[i][j]
return dp[-1][-1] # 가장 오른쪽 아래에 담긴 경우의 수를 return
print(sol())문제 출처
1890번: 점프
첫째 줄에 게임 판의 크기 N (4 ≤ N ≤ 100)이 주어진다. 그 다음 N개 줄에는 각 칸에 적혀져 있는 수가 N개씩 주어진다. 칸에 적혀있는 수는 0보다 크거나 같고, 9보다 작거나 같은 정수이며, 가장
www.acmicpc.net
728x90
반응형
'Study > Coding Test' 카테고리의 다른 글
| [백준 BOJ / Python] 1965번 상자넣기 DP (0) | 2023.02.06 |
|---|---|
| [백준 BOJ / Python] 25338번 바지 구매 math (0) | 2023.02.01 |
| [백준 BOJ / Python] 17404번 RGB거리 2 DP (0) | 2023.01.30 |
| [백준 BOJ / Python] 1149번 RGB거리 DP (0) | 2023.01.28 |
| [백준 BOJ / Python] 2565번 전깃줄 DP (0) | 2023.01.18 |
댓글

