티스토리 뷰
728x90
반응형
문제
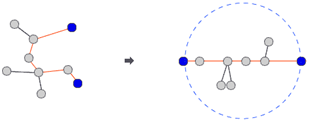
트리는 사이클이 없는 무방향 그래프이며, 두 노드 사이의 경로가 항상 하나만 존재한다.
두 노드를 선택하여 양쪽으로 쫙 당길 때, 가장 길게 늘어나는 경우를 트리의 지름이라고 한다.
입력으로는 루트가 있는 가중치가 있는 간선들로 이루어진 트리가 주어지며, 트리의 지름을 구하는 프로그램을 작성해야 합니다.
풀이
- 트리의 지름을 찾기 위해 DFS를 활용한다.
- 트리의 임의의 노드 $x$를 기준으로 잡는다.
- 노드 $x$로부터 노드 간 거리를 DFS를 통해 구하고, 거리가 가장 먼 노드 $y$를 찾는다.
- 노드 $y$를 기준으로 노드 간 거리를 다시 구한다.
- 거리가 가장 먼 노드 $z$를 찾는다.
- 노드 $y$와 노드$z$ 사이의 거리가 트리의 지름이다. (가장 큰 값을 출력하면 된다.)
◆ 트리의 지름 증명
트리의 지름 양쪽 끝 노드를 노드 $u$와 노드 $v$라고 가정한다.
임의의 노드 $x$를 정하고, 노드 $x$에서 가장 먼 노드 $y$를 찾았을 때 세 가지의 경우가 있다.
- $x$가 $u$ 혹은 $v$ 인 경우
- $y$가 $u$ 혹은 $v$인 경우
- $x, y, u, v$가 서로 다른 경우
1과 2의 경우에는 위의 풀이를 통해 '트리의 지름'을 구할 수 있음을 알 수 있다.
- 노드 $x$가 지름의 한쪽이라면 가장 먼 거리에 있는 노드 $y$가 다른 지름의 한쪽이 된다. (1)
- 마찬가지로 노드 $y$에서 다시 가장 먼 거리에 있는 노드 $z$는 결국 노드 $x$가 되고 $\bar{xy}$는 트리의 지름이 된다. (2)
3번 $x, y, u, v$가 서로 다른 경우에는 아래 두 가지 경우의 수가 있다.
(a) 노드 x와 노드 y를 연결하는 경로가 노드 u와 노드 v를 연결하는 경로가 한 점 이상 공유하는 경우
(b) 노드 x와 노드 y를 연결하는 경로가 노드 u와 노드 v를 연결하는 경로가 완전히 독립인 경우
* $d(x, t)$는 노드 $x$와 노드 $t$ 사이의 거리
(a)의 경우

- 알고리즘 조건에 따라 노드 $y$가 노드 $x$로부터 가장 먼 노드임으로, $d(t, y)$가 가장 길다.
- $ d(t, y) > d(t, u) $ and $ d(t, y) > d(t, v) $
- 트리의 지름은 $d(u,v)$ 이기 때문에 노드 $t$에서 가장 먼 노드는 $u$ 혹은 $v$가 되어야 한다.
- $d(t, u) > d(t, y) $ or $ d(t, v) > d(t, y)$
- 서로 더 길다고 하기 때문에 모순이 발생한다.
- 만약 $d(t,y) = max(d(t,u), d(t,v))$이라고 해도, $x, y, u, v$가 서로 다르다는 가정에 모순을 만든다.
(b)의 경우

- 알고리즘 조건에 따라 노드 $x$로부터 가장 먼 노드는 노드 $y$이기 때문에 $d(a, y)$가 가장 길다.
- $d(a, y)>d(a,b,u)$ and $ d(a, y) > d(a,b,v) $
- 트리의 지름은 $d(u,v)$ 이기 때문에 $d(b,u)$ 혹은 $d(b,v)$가 가장 길다.
- $d(b,u)>d(b,a,y)$ or $d(b,v) > d(b,a,y)$
- b의 경우도 a의 경우와 마찬가지로 서로가 더 길다고 주장하는 모순이 발생한다.
- 식을 합쳐보면 $d(a, y)>d(a,b,u) > d(b,a,y) $ => $d(a, y) > d(b,a,y) $ 이라는 모순을 볼 수 있다.
결론적으로 1번과 2번만 성립하고 3번은 모순이므로 $x, y, u, v$가 서로 다르지 않으며, $x, y$는 트리의 지름 양쪽 끝이 된다. 즉 트리의 지름은 다음과 같은 알고리즘을 통해 구할 수 있다.
- 임의의 노드 x를 정한다.
- 노드 x에서 가장 먼 노드 y를 찾는다.
- 노드 y에서 가장 먼 노드 z를 찾는다.
- 트리의 지름은 $d(y, z)$이다.
Python 코드
import sys
sys.setrecursionlimit(10 ** 9)
input = sys.stdin.readline
n = int(input())
# 양방향 그래프
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
p, c, w = map(int, input().split())
g[p].append((c, w))
g[c].append((p, w))
def dfs(x, w):
for next_node, wei in g[x]:
if distance[next_node] == -1:
distance[next_node] = w + wei
dfs(next_node, w + wei)
# 임의의 노드 루트를 기준으로 노드간 거리를 측정한다.
distance = [-1] * (n + 1)
distance[1] = 0
dfs(1, 0)
# 루트에서 가장 먼 노드를 기준으로 다시 노드간 거리를 측정한다.
start = distance.index(max(distance))
distance = [-1] * (n + 1)
distance[start] = 0
dfs(start, 0)
# 가장 먼 노드와의 거리를 출력한다.
print(max(distance))
문제출처
https://www.acmicpc.net/problem/1967
트리의 지름 증명 참고자료
728x90
반응형
'Study > Coding Test' 카테고리의 다른 글
| [백준 BOJ / Python] 10942번 팰린드롬 (0) | 2024.10.12 |
|---|---|
| [프로그래머스 / Python & Java] PCCP 기출문제 1번 / 동영상 재생기 (1) | 2024.09.20 |
| [백준 BOJ / Python] 1202번 보석 도둑 (0) | 2024.04.08 |
| [프로그래머스 / Python] 개인정보 수집 유효기간 (0) | 2024.01.02 |
| [프로그래머스 / Python] 미로 탈출 명령어 (DFS) (0) | 2023.11.26 |
댓글