티스토리 뷰
728x90
반응형
지난번까지는 한 줄로 나열된 데이터를 배웠다면, 이번에는 계층적으로 데이터를 다루려고 한다.
조직도나 파일 시스템처럼 부모-자식 관계를 가지는 트리(Tree)와 우선순위 관리에 최적화된 힙(Heap)을 통해 더 고급 수준으로 나아가 보자.
1. 트리의 기초와 순회 (Traversal)
트리를 눈으로 보고 순회 순서(전위/중위/후위)를 적어내거나, 코드를 보고 순서를 맞히는 문제가 나온다.
(1) 이진 트리 (Binary Tree) 핵심 용어
- 완전 이진 트리 (Complete Binary Tree): 위에서 아래로, 왼쪽에서 오른쪽으로 빈틈없이 채워진 트리. (힙의 필수 조건)
- 포화 이진 트리 (Full Binary Tree): 마지막 레벨까지 꽉 찬 트리. 높이가 $k$일 때, 노드 개수는 $2^k - 1$이다.
(2) 트리 순회 (Traversal) - 암기 필수!
루트(Root)를 언제 방문하느냐가 기준이다.
(A)
/ \
(B) (C)- 전위 순회 (Pre-order): [Root] $\rightarrow$ Left $\rightarrow$ Right
- 순서: A $\rightarrow$ B $\rightarrow$ C
- 코드 특징: print(n)이 재귀 호출보다 먼저 나옴.
- 중위 순회 (In-order): Left $\rightarrow$ [Root] $\rightarrow$ Right
- 순서: B $\rightarrow$ A $\rightarrow$ C
- 코드 특징: print(n)이 재귀 호출 사이에 껴 있음.
- 후위 순회 (Post-order): Left $\rightarrow$ Right $\rightarrow$ [Root]
- 순서: B $\rightarrow$ C $\rightarrow$ A
- 코드 특징: print(n)이 재귀 호출 뒤에 나옴.
1-2. 최신 기출 맛보기
문제. 다음 C언어 코드가 수행하는 트리 순회(Traversal) 방식은?
void Course(node *n) {
if (n != NULL) {
Course(n->left);
Course(n->right);
printf("%c ", n->name);
}}- 후위 순회
- 레벨 순서 순회
- 중위 순회
- 전위 순회
더보기
정답: 1번
- 재귀 호출의 순서: 왼쪽 $\rightarrow$ 오른쪽 $\rightarrow$ 루트
- 루트를 가장 나중에 방문하므로 후위 순회이다.
- Tip!
- printf가 맨 앞에 있으면: 전위 순회 (Pre-order)
- printf가 중간에 있으면: 중위 순회 (In-order)
- printf가 맨 뒤에 있으면: 후위 순회 (Post-order)
2. 힙 (Heap) - 데이터직 시험 최다 빈출
힙은 우선순위 큐를 구현하는 가장 효율적인 자료구조이다. 배열 인덱스 계산, 삽입/삭제 과정, 시간 복잡도가 출제 포인트다.
(1) 힙의 정의
- 최대 힙 (Max Heap): 부모 $\ge$ 자식. (루트가 가장 큰 값)
- 구조: 반드시 완전 이진 트리여야 함.
(2) 배열로 구현 (중요!)
힙은 구멍 없이 꽉 차 있으므로 배열이 가장 효율적입니다. (연결리스트 X)
- 인덱스 계산 공식 (기준 인덱스가 $i$일 때) :
- 왼쪽 자식: $2 \times i$
- 오른쪽 자식: $2 \times i + 1$
- 부모: $i / 2$
[1]
/ \
[2] [3]
/ \
[4] [5]
배열: [1, 2, 3, 4, 5]
인덱스:[0, 1, 2, 3, 4]
기준 인덱스가 1일 때, 왼쪽 자식의 인덱스는 2, 오른쪽 자식의 인덱스는 3, 부모의 인덱스는 0이다.
(3) 핵심 연산과 시간 복잡도
| 연산 | 과정 | 시간 복잡도 |
| 삽입 (Insert) | 맨 끝에 넣고 부모와 비교하며 올라감 (Up-Heap) | $O(\log n)$ |
| 삭제 (Delete) | 루트 제거 $\rightarrow$ 맨 끝 원소를 루트로 이동 $\rightarrow$ 자식과 비교하며 내려감 (Down-Heap) |
$O(\log n)$ |
| 확인 (Peek) | 최댓값/최솟값 확인 (루트만 보면 됨) | $O(1)$ |
| 힙 정렬 (Heap Sort) | 힙 생성($O(n)$) + $n$번 삭제($O(n \log n)$) | 전체 $O(n \log n)$ |
- Up-Heap: 맨 끝에서부터 내 부모(Index/2)와 나(Index)를 비교해 조건을 만족할 때까지 자리를 바꾸며(Swap) 올라간다.
- Down-Heap: 막내를 루트로 옮기고, 루트부터 자식 중 더 작은/큰 값과 비교해 조건을 만족할 때까지 Swap 하며 내려간다.
- 힙 생성: 일단 무작위로 넣고 리프 노드의 부모부터(제일 아래 층부터 올라가면서) Down-Heap을 하는 것이라고 보면 된다.
- 힙 정렬은 힙을 사용한 정렬로 일한 힙을 생성하고 하나씩 삭제하며서 제일 작은/큰 수부터 정렬하는 방법
2-2. 최신 기출 맛보기
문제. 힙(Heap) 자료구조의 시간 복잡도에 대한 설명으로 옳은 것은?
- 힙 생성(Build Heap) 후, 데이터 1개를 삽입하는 데 걸리는 시간은 $O(1)$이다.
- 힙 정렬(Heap Sort)의 전체 시간 복잡도는 최악의 경우 $O(n^2)$이다.
- 루트 노드(최댓값/최솟값)를 삭제하고 힙 속성을 다시 만족시키는 데 $O(\log n)$이 걸린다.
- 힙에서 최댓값(또는 최솟값)을 확인(Peek)하는 데는 $O(\log n)$이 걸린다.
더보기
정답: 3번
- 삽입은 트리의 높이만큼 올라가야 하므로 $O(\log n)$이다.
- 힙 정렬은 최악의 경우에도 $O(n \log n)$을 보장한다. (병합 정렬과 동일)
- 삭제 후 재정렬(Down-Heap) 과정은 트리의 높이($\log n$)만큼 걸린다.
- 힙의 대장(최대/최소)은 항상 루트에 있으므로 확인은 $O(1)$이다.
3. 이진 탐색 트리 (BST)
탐색 원리와 노드 삭제 시 누구랑 자리를 바꾸는지가 핵심이다.
(1) 정의
- 규칙: Left < Root < Right 왼쪽은 나보다 작고, 오른쪽은 나보다 크다.
- 특징: 중위 순회(In-order)하면 오름차순 정렬된 결과가 나온다. (10 -> 20 -> 30)
(2) 노드 삭제 (Deletion) - 까다로움
- 자식이 없으면? 그냥 삭제.
- 자식이 1개면? 자식을 내 자리로 올림.
- 자식이 2개면? (시험 포인트)
- 방법 1: 왼쪽 서브트리에서 가장 큰 놈 (Predecessor)
- 방법 2: 오른쪽 서브트리에서 가장 작은 놈 (Successor)
- 둘 중 하나를 데려와 자리를 채운다. (비슷한 값을 가져와야 트리가 안 깨짐)
3-1. 최신 기출 맛보기
문제. 다음 데이터를 순서대로 삽입하여 '이진 탐색 트리(BST)'를 생성한 후, '전위 순회(Pre-order)'한 결과는?
입력 데이터: [40, 20, 30, 10]
- 40, 30, 20, 10
- 40, 20, 10, 30
- 10, 20, 30, 40
- 40, 20, 30, 10
더보기
정답: 2번
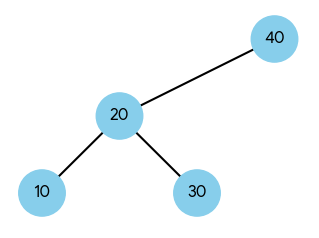
- 트리 생성 과정
- 40: 루트 노드
- 20: 40보다 작으므로 왼쪽에 넣음
- 30: 40보다 작으므로 왼쪽($\to$ 20)으로 갔다가, 20보다는 크므로 20의 오른쪽에 넣음.
- 10: 40보다 작고($\to$ 20), 20보다 작으므로 20의 왼쪽에 넣음.
- 트리 구조

- 전위 순회([루트] $\rightarrow$ 왼쪽 $\rightarrow$ 오른쪽): 40 -> 20 -> 10 -> 30.
- 40 (루트) 방문 $\rightarrow$ 출력: 40
- 왼쪽 서브트리(20)로 이동.
- 20 (부분 루트) 방문 $\rightarrow$ 출력: 20
- 20의 왼쪽(10)으로 이동.
- 10 방문 $\rightarrow$ 출력: 10
- 20의 오른쪽(30)으로 이동.
- 30 방문 $\rightarrow$ 출력: 30
4. [심화] 고급 균형 트리 (Balanced Tree)
최근 7급 시험은 여기서 변별력을 낸다.
(1) AVL 트리
- 개념: BST인데 좌우 높이 차이(Balance Factor)가 1 이하가 되도록 유지한다.
- 회전 (Rotation): 불균형 발생 시 LL, RR, LR, RL 회전으로 균형을 맞춘다.
- 원칙: "불균형이 발생한 곳(그랜드 부모)을 기준으로, 어디가 무거워졌는지 본다."
- LL / RR: 1번 회전 (Right / Left Rotate)
- LR / RL: 2번 회전 (방향 꺾어서 회전)
(2) B-트리
- 개념: 자식을 여러 개($M$개) 가질 수 있는 다차원 트리. (DB 인덱스에 사용)
- 삽입 규칙: 노드가 꽉 차면($M-1$개 초과, Overflow), 중간값(Median)이 부모로 승진(Split)하고 쪼개진다.
- 트리가 위로 자라는 것이 특징
- 2-3트리는 자식이 최대 3개인 B-트리
(3) 레드-블랙 트리 (Red-Black Tree)
- 조건 암기:
- 루트는 무조건 검은색(Black).
- 빨간색 노드의 자식은 무조건 검은색 (No Double Red).
- 모든 리프(NIL: 검정 벽)까지 가는 경로의 검은색 노드 개수는 동일(Black Height).
- (추가)
- 삽입은 일단 무조건 빨간색 이후 Red-Red이면 회전하거나 색을 반전한다.
- 삼촌(부모의 형제)도 Red면 색 반전
- 삼촌이 Black(or NIL)이면 회전
- 빨간 노드는 지워도 상관 없음. 검정 노드를 지우면 재조정 필요!
- 형제 노드 색을 보고 회전하고 빨간 조카를 검정으로 만들어 검정하나를 넘겨받거나
- Red-Red가 아니라는 보장하에 검정 노드를 빨강으로 바꾼다.
- 삽입은 일단 무조건 빨간색 이후 Red-Red이면 회전하거나 색을 반전한다.
5. 기타 특수 트리
- 허프만 트리 (Huffman Tree): 빈도수가 높은 문자는 짧게, 낮은 문자는 길게 비트를 할당하는 압축 알고리즘. (탐욕(Greedy) 기법)
- 시험에서는 단서 조항이 붙기에 주의하면서 풀자!
- 압축 과정은 빈도수가 낮은 것부터 합쳐서 올라가기.
- 압축한 트리를 보면서 각 알파벳에 대한 코드를 구하고 알파벳을 코드로 바꿔서 나열.
- 디코딩은 반대로 트리를 보고 각 알파벳에 대한 코드를 구하고 하나씩 매칭해서 문자열 도출.
- 트라이 (Trie): 문자열 검색에 최적화된 트리.
- 시간 복잡도는 문자열 길이에 비례($O(L)$).
- 접두사(Prefix)를 공유해서 저장 공간을 아끼고 검색 속도 높이는 N진 트리.
- 단점: 각 노드마다 자식 포인터(알파벳 26개 등)를 배열로 가지고 있어야 해서 메모리를 많이 차지.
- TEA, TEN, IN, ANT 가 있다면 아래와 같이 트리 구성 가능.
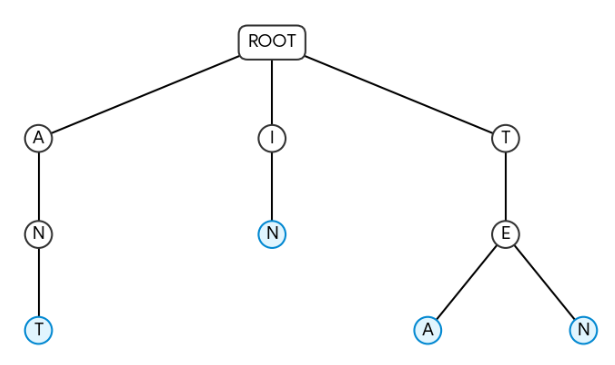
👉 고급 트리 관련 기출 문제를 풀어보고 싶다면? 제미나이가 만든 퀴즈 풀어보기
다음 포스팅에서는 그래프 탐색에 대해 정리해 보겠다.
728x90
반응형
'Study' 카테고리의 다른 글
| [전산직(데이터) 공무원 대비] 알고리즘 기초부터 파헤치기 3 (0) | 2026.01.19 |
|---|---|
| [전산직(데이터) 공무원 대비] 알고리즘 기초부터 파헤치기 2 (0) | 2026.01.17 |
| [전산직(데이터) 공무원 대비] 알고리즘 기초부터 파헤치기 1 (0) | 2026.01.17 |
| [Python / Java / C] 조건문 if문, if-else문, if-elseif-else문 (0) | 2023.06.15 |
댓글
