티스토리 뷰
728x90
반응형
문제
그래프의 정점을 두 집합으로 분할할 때, 인접한 정점끼리 서로 다른 집합에 포함되는 그래프를 이분 그래프라고 한다. 주어진 그래프가 이분 그래프인지 판별하는 문제이다.
풀이
- 이분 그래프인지 확인하기 위해서 정점들을 두 가지 색으로 칠할 때, 인접한 정점끼리 서로 다른 색으로 칠할 수 있는지를 확인하면 된다. 즉, 인접한 정점이 같은 색이라면 이분 그래프가 아닌 것이다.
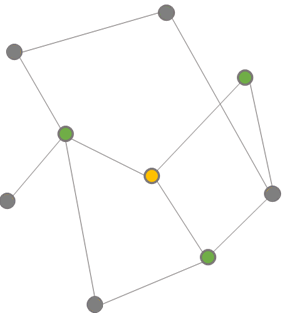
- 예를 들어 a를 노란색(1)으로 칠한다면, a와 연결된 b,c,d를 초록색(2)으로 칠하는 것이다.
- 그 다음 b,c,d에 연결된 인접한 정점들을 다시 노란색(1)로 칠하다가 이미 다른 색으로 칠해진 정점을 만났을 때, b,c,d와 같은 초록색(2)이 칠해져 있다면 이분 그래프가 아니라고 판별할 수 있다. 반대로 모든 정점들을 방문해도 이상이 없었다면 이분 그래프인 것이다.
[알고리즘] 이분 그래프 (Bipartite Graph)
인접한 노드(정점)끼리 서로 다른 색으로 칠해서 두 가지 색으로 분할할 수 있는 그래프를 이분 그래프라고 한다. 즉 각각의 집합에 속한 노드끼리는 서로 인접하지 않도록 분할하는 것이다. 시
code-angie.tistory.com
알고리즘
- 양방향 그래프를 입력받는다.
- BFS를 사용하여 모든 정점(노드)를 탐색하면서 인접한 노드들의 색을 칠하며 이분 그래프인지 판별해나간다.
Python 코드
from collections import defaultdict, deque
import sys
input = sys.stdin.readline
def sol():
v,e = map(int,input().split())
color = [0]*(v+1) # 칠해줄 색을 담을 곳
g = defaultdict(list)
# 양방향 그래프
for _ in range(e):
x,y = map(int,input().split())
g[x].append(y)
g[y].append(x)
# 모든 노드 탐색
for i in range(1,v+1):
if color[i]: # 이미 지나온 노드면 넘어가기
continue
# 새로 접한 노드면 색을 칠해주고 인접한 노드들 탐색
color[i] = 1
q = deque([i])
while q:
now = q.popleft()
next_color = color[now] % 2 + 1 # 다음 노드의 색 (색은 1 혹은 2)
for next in g[now]:
# 아직 방문하지 않았다면
if not color[next]:
color[next] = next_color
q.append(next)
# 만약 인접 노드가 현재 노드와 같은 색이라면 이분 그래프가 아님
elif color[next] != next_color:
return "NO"
# 끝까지 이상 없으면 아직은 이분 그래프
return "YES"
k = int(input())
for _ in range(k):
print(sol())문제 출처
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
728x90
반응형
'Study > Coding Test' 카테고리의 다른 글
| [백준 BOJ / Python] 27377번 읽씹 멈춰! Greedy (그리디) (0) | 2023.02.18 |
|---|---|
| [백준 BOJ / Python] 1806번 부분합 Prefix Sum (누적합) (0) | 2023.02.15 |
| [백준 BOJ / Python] 25194번 결전의 금요일 DP (0) | 2023.02.07 |
| [백준 BOJ / Python] 1965번 상자넣기 DP (0) | 2023.02.06 |
| [백준 BOJ / Python] 25338번 바지 구매 math (0) | 2023.02.01 |
댓글

