티스토리 뷰
728x90
반응형
문제
새로운 언어로 암호화된 문장을 해석하는데 드는 비용의 최솟값을 구하는 문제이다.
이 문장은 연속된 단어의 연결로 이루어져 있으며, 단어는 0번 이상 쓰일 수 있다. 또한 각 단어는 알파벳의 순서를 바꾸어 암호화되었을 수 있다. 이러한 문장을 해석하는 비용은 원래 단어의 위치와 다른 위치에 있는 알파벳 개수만큼 든다.
예를 들어 원래 단어가 one 이라면, oen은 비용이 2만큼, neo는 비용이 3만큼 든다.
풀이
- 암호화는 한 단어 내에서 알파벳의 위치만 변한 것이다. 따라서 문장 내에 주어진 단어가 포함된다면 그 단어의 길이만큼 문장을 잘랐을 때, 주어진 단어의 알파벳을 정렬한 결과와 문장에서 잘린 부분의 알파벳 정렬 결과가 동일해야 한다.
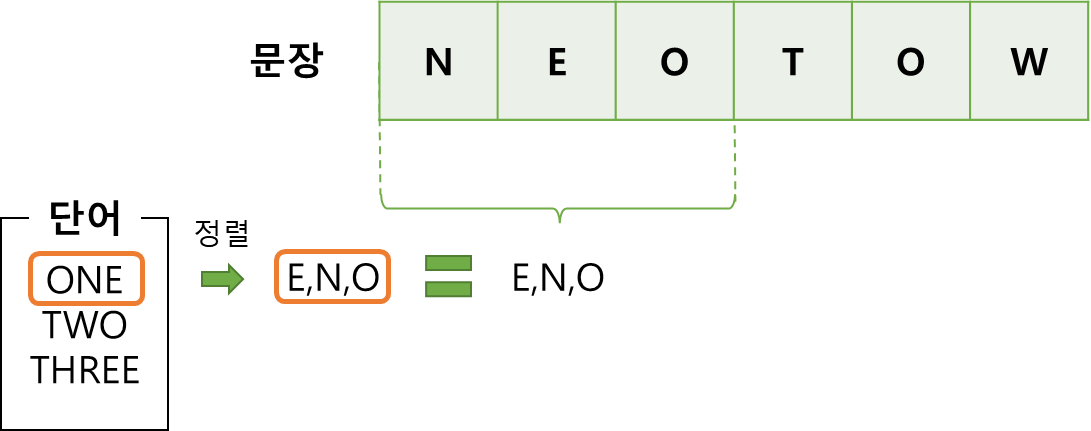
- 정렬 결과가 같다면 주어진 단어를 만들 수 있음으로 해석 비용을 계산한다.
- 단어에 대한 해석 비용은 주어진 단어(one)와 문장 일부(neo)의 알파벳을 하나씩 비교하여 서로 다른 알파벳인 경우의 수를 계산하여 구한다.
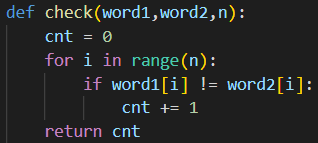
- 문장은 단어의 연속으로 이루어져 있기에 앞에서부터 최소 비용을 만족하는 단어들을 채워나가야 한다.
- 이때 주어진 단어의 길이가 다양하고 여러 번 쓰일 수 있음으로 2차원 배열을 활용한 DP를 통해 문제를 풀 수 있다.
- 최소 비용을 계산하는 점화식은 다음과 같다.
- dp[ 단어의 시작 위치 i ][ i 부터 단어의 끝 ]
= min( dp[i][i+len(word)-1], i 이전 단어까지의 최소 비용 + i번째에 매치 가능한 단어의 해석 비용 ) - l = len(word)
- dp[i][i+l-1] = min(dp[i][i+l-1], dp[i-1][0] + check(s[i:i+l], word, l))
- dp[ 단어의 시작 위치 i ][ i 부터 단어의 끝 ]
- 여기서 이전 단어까지의 최소 비용을 쉽게 가져오기 위해 단어의 끝 위치에 해당 단어까지의 최소 비용을 담는다.
- dp[i+l-1][0] = min(dp[i+l-1][0],dp[i][i+l-1])

알고리즘
- 해석 비용 함수를 정의한다.
- 두 단어의 알파벳을 순환하면서 같지 않은 경우 비용을 1씩 추가한다.
- 문장 s를 입력 받는다. (이후 계산을 위해 앞에 공백을 하나 추가한다.)
- 주어지는 단어의 개수 n을 정의하고 words 리스트에 단어 목록을 입력받는다.
- 최소 비용을 담을 큰 수가 입력된 2차원 배열 DP를 생성한다.
- dp[0][0]을 0으로 초기화 한다. (시작 이전 위치의 비용)
- 문장의 모든 위치를 순회하면서 바로 앞에 이어질 단어가 존재하지 않는다면 다음 위치로 이동하고,
존재한다면 words 리스트의 단어들을 비교하며 해석 가능한 단어라면 최소 비용을 계산한다. - 문장의 마지막 위치까지 비용이 계산되었다면 해당 최소 비용을 출력하고, 아니라면 -1을 출력한다.
Python 코드
import sys
input = sys.stdin.readline
# 단어 해석 비용 함수
def check(w1,w2,l):
cnt = 0
for i in range(l):
if w1[i] != w2[i]:
cnt+=1
return cnt
s = " "+input().strip()
n = int(input())
words = [input().strip() for _ in range(n)]
dp = [[1000]*(len(s)) for _ in range(len(s))]
dp[0][0] = 0
for i in range(1,len(s)+1):
if dp[i-1][0] == 1000: # 앞서 연결될 수 있는 단어가 없음
continue
for word in words:
l = len(word)
if sorted(s[i:i+l]) == sorted(word): # 해석될 수 있는 단어
dp[i][i+l-1] = min(dp[i][i+l-1],dp[i-1][0]+check(s[i:i+l],word,l))
# 맨 앞에 현재 길이까지의 최솟값을 업데이트 해주기
dp[i+l-1][0] = min(dp[i+l-1][0],dp[i][i+l-1])
if dp[-1][0] != 1000:
print(dp[-1][0])
else: # 해석 불가능함
print(-1)문제출처
1099번: 알 수 없는 문장
첫째 줄에 문장이 주어진다. 문장의 길이는 최대 50이다. 둘째 줄에 단어의 개수 N이 주어지며, N은 50보다 작거나 같은 자연수이다. 셋째 줄부터 N개의 줄에 각 단어가 주어진다. 단어의 길이는 최
www.acmicpc.net
728x90
반응형
'Study > Coding Test' 카테고리의 다른 글
| [백준 BOJ / Python] 14002번 가장 긴 증가하는 부분 수열 4 DP (0) | 2023.02.23 |
|---|---|
| [백준 BOJ / Python] 10986번 나머지 합 (누적합) (0) | 2023.02.21 |
| [백준 BOJ / Python] 27377번 읽씹 멈춰! Greedy (그리디) (0) | 2023.02.18 |
| [백준 BOJ / Python] 1806번 부분합 Prefix Sum (누적합) (0) | 2023.02.15 |
| [백준 BOJ / Python] 1707번 이분 그래프 (Bipartite Graph) (0) | 2023.02.11 |
댓글

