티스토리 뷰
728x90
반응형
- 배열의 일부 구간에 대한 합을 빠르게 구할 수 있는 알고리즘이다.
- 배열의 값들이 변하지 않는다면 누적된 합 또한 변동이 없다는 점을 적용한다.
- 미리 구해둔 누적합을 통해 배열 중 특정 구간의 부분합을 쉽게 구할 수 있다.
- 값을 미리 저장해 두는 점이 DP와 유사하다.
< 누적합의 조건 >
- 배열의 값들이 변하지 않음
1. 1차원 누적합 알고리즘
1.1. 1차원 누적합
- 그림과 같이 앞에서부터 차례대로 누적된 합계를 prefixSum 배열에 저장한다.
- 첫 번째(0) 값은 arr 값과 prefixSum 값이 동일하다.
- 현재 위치(i)의 arr 값에 prefixSum 배열에 저장된 직전 위치(i-1)까지의 합을 더하여 현재 위치의 누적합을 구하여 prefixSum에 입력한다.
- 점화식은 다음과 같다.
- prefixSum[i] = prefixSum[i-1] + arr[i]
1.1.1. 1차원 누적합 python 코드
- 시간복잡도: O(n)
def prefix_sum(n):
prefixSum = [0]*n # prefixSum을 담을 빈 배열 생성
prefixSum[0] = arr[0] # 첫번째 값을 넣어줌
for i in range(1,n): # 두번째 값부터 누적합을 저장
prefixSum[i] = prefixSum[i-1] + arr[i]
return prefixSum
n = int(input())
arr = list(map(int, input().split()))
prefixSum = prefix_sum(n)
1.2. 1차원 부분합
- 3에서 6까지의 부분합을 구하려면 6까지의 합 28에서 2까지의 합 9를 빼면 된다.
- 즉, i ~ j까지의 합은 j까지의 누적합 - (i-1)까지의 누적합 (i번째 값 포함)을 계산한 값이 된다.
- 점화식은 다음과 같다.
- partSum = prefixSum[j] - prefixSum[i-1]
1.2.1. 1차원 부분합 python 코드
- 시간복잡도: O(1)
n,m = map(int, input().split())
arr = [list(map(int, input().split())) for _ in range(n)]
s = prefix_sum(n,m) # 누적합을 구함
i,j = map(int,input().split())
partSum = prefixSum[j] - prefixSum[i-1]
print(partSum)
2. 2차원 누적합 알고리즘
2.1. 2차원 누적합
- 2차원의 배열에서 1번 빨간색 구역인 (i, j)까지의 누적합은 3번 초록색 구역과 4번 노란색 구역의 합에서 겹치는 부위인 2번 파란색 구역을 제외하고 새롭게 (i, j)에 해당하는 5번 갈색 구역의 값을 더하여 구한다.
- 점화식을 원활하게 계산하기 위하여 prefixSum에 행과 열을 하나씩 추가하여 빈칸 즉 0으로 채우는 방법을 사용할 수 있다.
- 이때, arr 보다 prefixSum의 인덱스가 1씩 큰 것을 주의해야 한다.
- 점화식은 다음과 같다.
- prefixSum[i][j] = prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1] + arr[i-1][j-1]

- 예를 들어 위와 같은 배열 arr이 주어졌을 때, 빨간색 구역의 누적합은
- arr의 초록색 구역의 누적합, 즉 prefixSum에서의 초록색 동그라미로 표시된 6을 더하고
- arr의 노란색 구역의 누적합, prefixSum에서의 노란색 동그라미로 표시된 8을 더하고
- arr의 파란색 구역의 누적합, prefixSum에서의 파란색 동그라미로 표시된 4를 빼고
- 마지막으로 arr의 갈색 동그라미로 표시된 3을 더해줌으로써 구할 수 있다.
2.1.1. 2차원 누적합 python 코드
- 시간복잡도: O(N**2)
def prefix_sum(n,m):
prefixSum = [[0]*(m+1) for _ in range(n+1)]
for i in range(1,n+1):
for j in range(1,m+1):
prefixSum[i][j] = prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1] + arr[i-1][j-1]
return prefixSum
n,m = map(int, input().split())
arr = [list(map(int, input().split())) for _ in range(n)]
prefixSum = prefix_sum(n,m)
2.2. 2차원 부분합
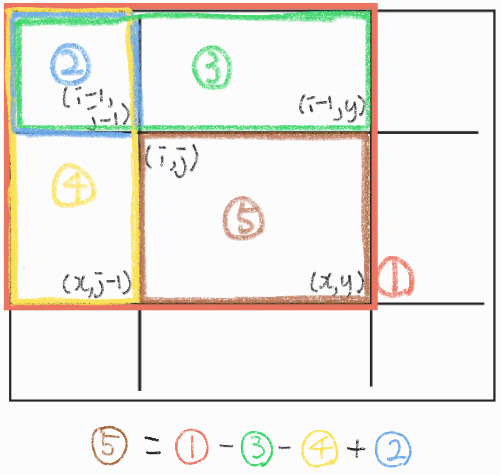
- 누적합을 사용하여 (i,j)에서 (x,y)까지의 부분합을 쉽게 구할 수 있다.
- 5번 갈색 구역의 부분합을 구하기 위해서는
- 1번 빨간색 (x,y)의 누적합에서
- 3번 초록색 (i-1,y)의 누적합을 빼고,
- 4번 노란색 (x,j-1)의 누적합을 빼고,
- 중복으로 제외된 2번 파란색 (i-1,j-1)의 누적합을 더한다.
- 점화식은 다음과 같다.
- partSum = prefixSum[x][y] - prefixSum[i-1][y] - prefixSum[x][j-1] + prefixSum[i-1][j-1]
2.2.1. 2차원 부분합 python 코드
- 시간복잡도: O(1)
n,m = map(int, input().split())
arr = [list(map(int, input().split())) for _ in range(n)]
prefixSum = prefix_sum(n,m)
i,j,x,y = map(int,input().split())
# (i,j)칸에서 (x,y)칸까지 포함한 부분합
partSum = prefixSum[x][y] - prefixSum[i-1][y] - prefixSum[x][j-1] + prefixSum[i-1][j-1]
print(partSum)728x90
반응형
'Study > Algorithm' 카테고리의 다른 글
| [알고리즘 / Python] 최소신장트리 (크루스칼 알고리즘) (0) | 2023.04.14 |
|---|---|
| [알고리즘 / Python] 분리집합 (Disjoint Set / 서로소 집합) (0) | 2023.03.17 |
| [알고리즘] 이분 그래프 (Bipartite Graph) (0) | 2023.02.09 |
| [알고리즘 / Python] 동적프로그래밍 (DP, Dynamic Programming) (0) | 2023.01.20 |
| [알고리즘 / Python] 이분 탐색 / 이진 탐색 (Binary Search) (3) | 2023.01.17 |
댓글