티스토리 뷰
728x90
반응형
1. 분리집합 (Disjoint Set)
- 분리집합은 서로 겹치는 원소가 없는 상호 배타적인 집합들을 의미하며 서로소 집합이라고도 불린다.
- 전체 집합에 대하여 겹치지 않는 두 개 이상의 부분 집합이라 할 수 있다.
- 즉, 분리집합 알고리즘은 각 원소가 속하는 부분 집합을 찾아 분리를 하는 것이다.
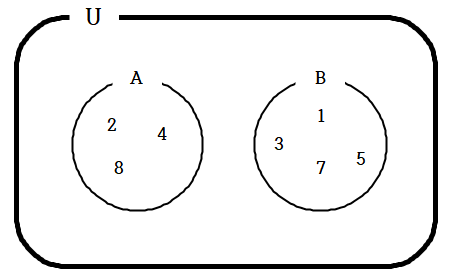
- 예를 들어, 전체 집합 U에 대하여 짝수 집합 A와 홀수 집합 B는 서로 겹치는 원소가 없는 부분 집합들로 분리집합이라 할 수 있다.
2. Union-Find 알고리즘
- 시간복잡도: 평균적으로 O(logN)이며, 최악의 경우에는 O(n)이다.
- 트리구조를 사용한다. 하지만 이때, 자식노드가 부모노드 가리킨다는 것에 차이가 있다.
- 두 개 노드가 있을 때, 서로 같은 집합에 있는지 아닌지 판별하는 알고리즘이다.
- Find 함수는 루트를 찾아들어가 x노드가 속한 집합을 찾는 역할을 한다.
- Union 함수는 x노드와 y노드의 집합을 합치는 역할을 한다.
- 마지막까지도 합쳐지지 않는 노드들이 있다는 것은 서로 겹치지 않는 집합이 존재한다는 것을 의미한다.
2.1. Find 함수
parent = list(range(n+1)) # 초기화
def find(x):
# 자신이 루트이면 자기 자신 반환
if x == parent[x]:
return x
# 자신이 루트가 아니면 부모를 루트로 만듦
else:
parent[x] = find(parent[x])
return parent[x]2.2. Union 함수
# 기본
def union(x,y):
# 부모 노드 탐색
x = find(x)
y = find(y)
# 부모를 합칠 때 더 작은 값 쪽으로 합침
if y < x:
parent[x] = y
else:
parent[y] = x
# rank 사용
rank = list(range(n+1))
def union(x,y):
# 부모 노드 탐색
x = find(x)
y = find(y)
if x == y:
return
# 부모를 합칠 때 더 작은 값 쪽으로 합침
if rank[x] < rank[y]:
a, b = y, x
else:
a, b = x, y
if rank[x] == rank[y]:
rank[b] += 1
parent[a] = b 728x90
반응형
'Study > Algorithm' 카테고리의 다른 글
| [Python / 알고리즘] Flood Fill 알고리즘 (0) | 2024.11.10 |
|---|---|
| [알고리즘 / Python] 최소신장트리 (크루스칼 알고리즘) (0) | 2023.04.14 |
| [알고리즘 / Python] 누적합 (Prefix Sum) (0) | 2023.02.13 |
| [알고리즘] 이분 그래프 (Bipartite Graph) (0) | 2023.02.09 |
| [알고리즘 / Python] 동적프로그래밍 (DP, Dynamic Programming) (0) | 2023.01.20 |
댓글
