티스토리 뷰
728x90
반응형
동적프로그래밍
- 동적 프로그래밍은 큰 문제를 작은 문제로 나누어 푸는 방법이다.
- 분할 정복과는 다르게 작은 문제를 푸는데서 답이 같은 문제가 중복적으로 일어날 경우 사용한다.
- 보통 점화식을 만들 수 있다.
1. 동적프로그래밍의 조건
- 큰 문제는 작은 문제로 나눌 수 있고 작은 문제가 반복해서 나타난다.
- 같은 문제라면 계산할 때마다 같은 답이 도출된다.
2. 메모이제이션 (Memoization)
- 메모이제이션은 한번 풀었던 작은 문제를 다시 반복해서 풀지 않기 위해 메모해두고 필요할 때 답만 꺼내 보는 것이다.
- 담아 놓는 것이기 때문에 캐싱 (caching) 이라고도 불린다.
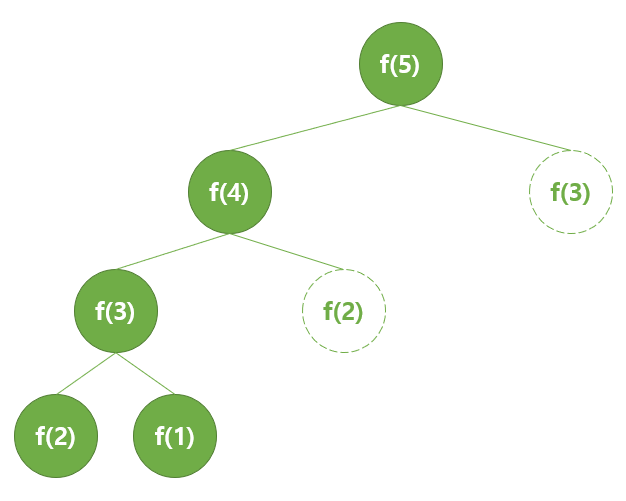
- 메모이제이션을 통해 먼저 구한 결과를 담아 두면, 아래 피보나치 예시에서 점선으로 표시된 노드는 먼저 먼저 계산된 값을 사용하면 되기 때문에 반복해서 계산하지 않아도 된다.
3. 기존 피보나치 함수 (재귀)
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(x - 1) + fibo(x - 2)4. 메모이제이션을 사용한 피보나치 함수
memo = [0] * (x+1)
def fibo(x):
if x == 1 or x == 2:
return 1
# 이미 계산한 경우 그 답 사용
if memo[x]:
return memo[x]
# 아니라면 새로 계산해서 답을 넣어줌
memo[x] = fibo(x - 1) + fibo(x - 2)
return memo[x]5. 동적프로그래밍(DP) 알고리즘
5.1. Top-down : 큰 문제에서 분할해 작은 문제를 푸는 방법
- 위의 피보나치 함수도 Top-down 방식이다.
- 보통 재귀함수로 구현한다.
- 가독성이 좋다.
memo = [0] * (x+1) def fibo(x): if x == 1 or x == 2: return 1 if memo[x]: return memo[x] memo[x] = fibo(x - 1) + fibo(x - 2) return memo[x]
5.2. Bottom-up : 작은 문제부터 차례로 풀어가는 방법
def fibo(x):
memo = [0] * (x+1)
memo[0] = 1
memo[1] = 1
for i in range(2,x+1):
memo[i] = memo[i-1] + memo[i-2]
return memo[x]6. DP 관련 응용 문제
728x90
반응형
'Study > Algorithm' 카테고리의 다른 글
| [알고리즘 / Python] 분리집합 (Disjoint Set / 서로소 집합) (0) | 2023.03.17 |
|---|---|
| [알고리즘 / Python] 누적합 (Prefix Sum) (0) | 2023.02.13 |
| [알고리즘] 이분 그래프 (Bipartite Graph) (0) | 2023.02.09 |
| [알고리즘 / Python] 이분 탐색 / 이진 탐색 (Binary Search) (3) | 2023.01.17 |
| [알고리즘 / Python] 가장 긴 증가하는 부분 수열 (LIS) (0) | 2023.01.16 |
댓글
